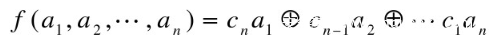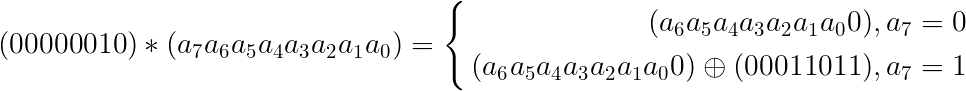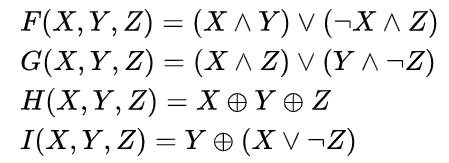FXTi's blog
0%

加密学-学校课程内容

Posted on Edited on

学校课程设涉及到的加密学算法实现

学校内容的加密学报告备份

古典密码

凯撒密码

凯撒密码是一种但表带换密码，因为罗马共和时期的凯撒曾用这种方法加密与将领们的信息而得名。狭义上，恺撒密码特指偏移量为3的情况。广义上，恺撒密码可以指所有在字母表上向后（或向前）按照一个固定数目进行偏移的密码。

举个例子当偏移量为+3时，A会变成D,C会变成F，等等。

加密实现

首先计算机实现中每个字符都有对应的码值，在Python中可以用ord()函数得到字符对应的ASCII码值。

可以得到加密的公式为：$c_i = (m_i + j) mod 26$

1
2
3
4
5
6
7
8
9
10
11
def encrypt(m, k):
    k %= 26
    res = ""
    for i in range(len(m)):
        if m[i].isupper():
            res += chr((ord(m[i])-ord('A')+k)%26+ord('A'))
        elif m[i].islower():
            res += chr((ord(m[i])-ord('a')+k)%26+ord('a'))
        else:
            res += m[i]
    return res

解密实现

解密过程就是加密过程的逆运算，对应公式为：$m_i = (c_i - k + 26) mod 26$

1
2
3
4
5
6
7
8
9
10
11
def decrypt(c,k):
    k %= 26
    res = ""
    for i in range(len(c)):
        if c[i].isupper():
            res += chr((ord(c[i])-ord('A')+26-k)%26+ord('A'))
        elif c[i].islower():
            res += chr((ord(c[i])-ord('a')+26-k)%26+ord('a'))
        else:
            res += c[i]
    return res

针对凯撒的攻击

暴力枚举

因为可能的偏移值仅有25种，完全可以直接枚举得到所有可能性，然后人工分辨的到其中正确的明文。

1
2
3
def bruteforce(c):
    for i in range(1, 26):
		print decrypt(c, i)

安全性分析

即使对于唯密文攻击，凯撒密码也因为偏移值的取值空间过小而非常容易破解。对于密文规模较大的可以直接让计算机基于字典来选取25中可能性较大的情况来直接得到可用的偏移值完成破解。

仿射密码

仿射密码和凯撒密码同属于单表代换密码，但相对于凯撒密码的简单位移，仿射密码构成了一个线性方程来完成明文到密文的变换。

加密实现

仿射密码的加密过程表达成公式：$c_i = (k_1 * m_i + k_2) mod 26$,要求$k_1$和26互素，即$gcd(k_1, 26) = 1$。实际上仅有满足这个条件时，$|C| = |M|$，否则对于同一个密文会有多个明文对应，使得从密文得到明文的过程无法完成。

判断最大公约数可使用辗转相除法：

1
2
3
4
def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a%b)

然后完成加密代码：

1
2
3
4
5
6
7
8
9
10
11
12
def encrypt(m, k1, k2):
    if gcd(k1, 26) != 1:
        return None
    res = ""
    for i in range(len(m)):
        if m[i].isupper():
            res.append(chr((k1*(ord(m[i])-ord('A'))+k2)%26+ord('A')))
        elif m[i].islower():
            res.append(chr((k1*(ord(m[i])-ord('a'))+k2)%26+ord('a')))
        else:
            res.append(m[i])
    return res

解密实现

根据加密公式可得到解密公式：$m_i = k_1^{-1} * (c_i - k_2) mod 26$，该过程中值得一提的是$k_1^{-1}$这个值的计算过程。这里选用拓展欧几里得求逆元：

1
2
3
4
5
6
7
8
9
def exgcdInv(a,m):
    if gcd(a,m)!=1:
        return None
    u1,u2,u3 = 1,0,a
    v1,v2,v3 = 0,1,m
    while v3!=0:
        q = u3//v3
        v1,v2,v3,u1,u2,u3 = (u1-q*v1),(u2-q*v2),(u3-q*v3),v1,v2,v3
    return u1%m

然后可以得到解密函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
def decrypt(c, k1, k2):
    if gcd(k1, 26) != 1:
        return None
    k1 = exgcdInv(k1, 26)
    res = ""
    for i in range(len(c)):
        if c[i].isupper():
            res += chr((k1*(ord(c[i])-ord('A')+26-k2))%26+ord('A'))
        elif c[i].islower():
            res += chr((k1*(ord(c[i])-ord('a')+26-k2))%26+ord('a'))
        else:
            res += c[i]
    return res

针对仿射的攻击

穷举攻击

对于密文暴力枚举出所有的可能组合(共$\phi(26) * 26 - 1 = 311$种 )然后从中选出有意义的正确明文。

1
2
3
4
5
def bruteforce(c):
    for i in range(1, 26):
		if gcd(i, 26) == 1:
            for j in range(26):
                print(decrypt(c, i, j))

统计分析攻击

再截取密文足够长的情况下，因为明文和密文一一对应的关系，明文中所呈现的自然语言规律也会体现在密文中。

于是首先对于密文中出现的所有字符个数进行统计并排序，按照自然语言规律中的出现次序进行匹配和对应的解密然后从中选取合理的解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Node:
    def __init__(self,ch,cnt):
        self.ch = ch
        self.cnt = cnt
    def __lt__(self,other):
        return self.cnt > other.cnt
    
def static(c):
    cLower = c.lower()
    alphaNum = []

    for i in range(26):
        t = Node(chr(ord('a')+i),0)
        alphaNum.append(t)

    for i in range(len(c)):
        if cLower[i].isalpha():
            alphaNum[ord(ciperCopy[i])-ord('a')].cnt += 1

    alphaNum.sort()
    for i in range(26):
        if gcd(i,26) == 1:
            for j in range(26):
                if chr((4*i+j)%26+ord('a')) == alphaNum[0].ch:
                    print(decrypt(c,i,j))

安全性分析

因为密钥空间根据之前的计算仅311种，对于穷举攻击来说轻而易举，更何况统计攻击。所以在现代视角看来仿射密码的安全性极弱。

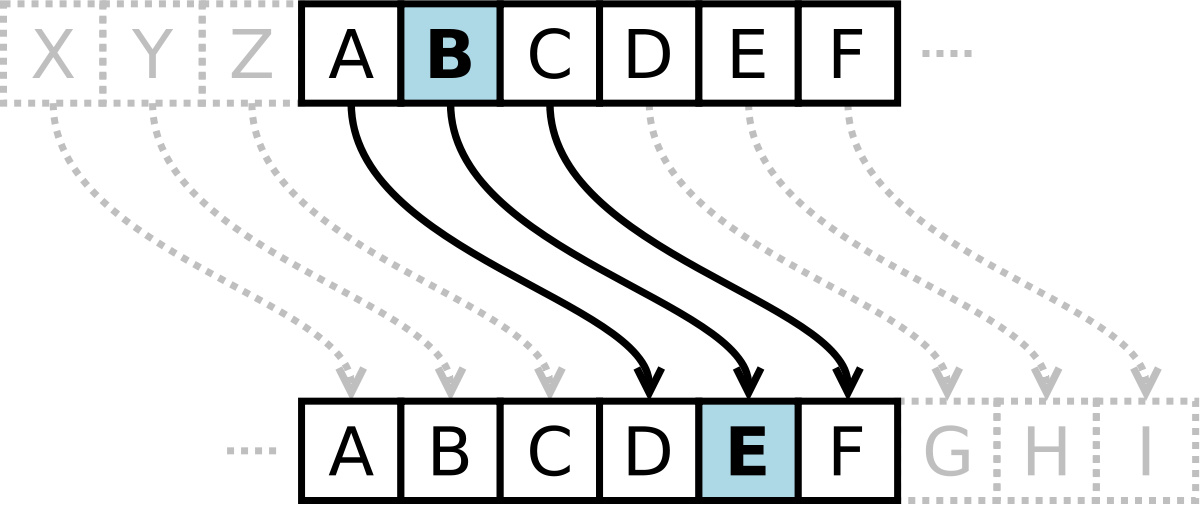
维吉尼亚密码

之前的密码都是单表替换密码，由于密钥空间过小而容易被破解。维吉尼亚密码则是多表替换密码，在同一段密码上使用多个替换过程来抗攻击。

对应的替换关系根据这一位对应的密钥所决定，公式：$c_i = (m_i + k_i) mod 26$，对应关系如图：

加密实现

1
2
3
4
5
6
7
m = input()
k = input().lower()

m = list(map(lambda x: (ord(x) - ord('A'), 'A') if 'A' <= x <= 'Z' else (ord(x) - ord('a'), 'a'), m))
#print(m)
c = [chr(((m[i][0]+(ord(k[i%len(k)]) - ord('a')))%26) + ord(m[i][1])) for i in range(len(m))]
print("".join(c))

解密实现

根据加密过程可推：$m_i = (c_i + 26 - k_i)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def decrypt(c,k):
    k = k.upper()
    j = 0
    res = ""
    for i in range(len(c)):
        if c[i].isupper():
            res += chr(((ord(c[i])-ord('A'))%26+26-(ord(k[j%len(k)])-ord('A'))%26)%26+ord('A'))
            j += 1
        elif c[i].islower():
            res += chr(((ord(c[i])-ord('a'))%26+26-(ord(k[j%len(k)])-ord('A'))%26)%26+ord('a'))
            j += 1
        else:
            res += c[i]
    return res

攻击方法

这里选用重合指数法破解维吉尼亚密码，其也要求有大段的密文来进行统计得到规律。
详细过程可以看PPT

重合指数：设某种语言由$n$个字母组成，每个字母i发生的概率为$p_i(1≤i≤n)$，则重合指数就是指两个随机字母相同的概率，记为$IC = \sum_{i=1}^{n}p_i$

一般用$IC$的无偏估计值$IC’$来近似计算$IC$. 其中的$x_i$表示字母$i$出现的频次，$L$表示文本长度，$n$表示某种语言中包含的字母数。$IC’=\sum_{i=1}^{n}\frac{x_i(x_i-1)}{L(L-1)}$

随机英文文本的$IC’$总是大约为0.038.
而一段有意义的英文文本的$IC’$总是大约为0.065.

而维吉尼亚加密是多表加密，则在每一张表加密的密文中仍应该服从自然语言规律。所以可以尝试去分割密文然后统计各张表上对应的密文是否符合规律并猜测得到表的数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
c = input().upper()

res = dict()
#for i in range(1,len(c)):
for i in range(1,min(128, len(c))):
    tlist = []
    for tmp in split(c,i):
        alpha = dict()
        for z in range(26):
            alpha[chr(ord('A')+z)] = 0
        for x in tmp:
            alpha[x] += 1
        acc = 0
        for ke in alpha.keys():
            acc += alpha[ke] * (alpha[ke] - 1)
        if len(tmp) > 1:
            tlist.append(acc / (len(tmp) * (len(tmp) - 1)))
    #print(str(i) + " " + str(tlist))
    res[i] = sum(tlist) / len(tlist)

# 0.065

ss = sorted(res.items(), key=lambda a: abs(a[1] - 0.065))[:10]
pprint.pprint(ss)

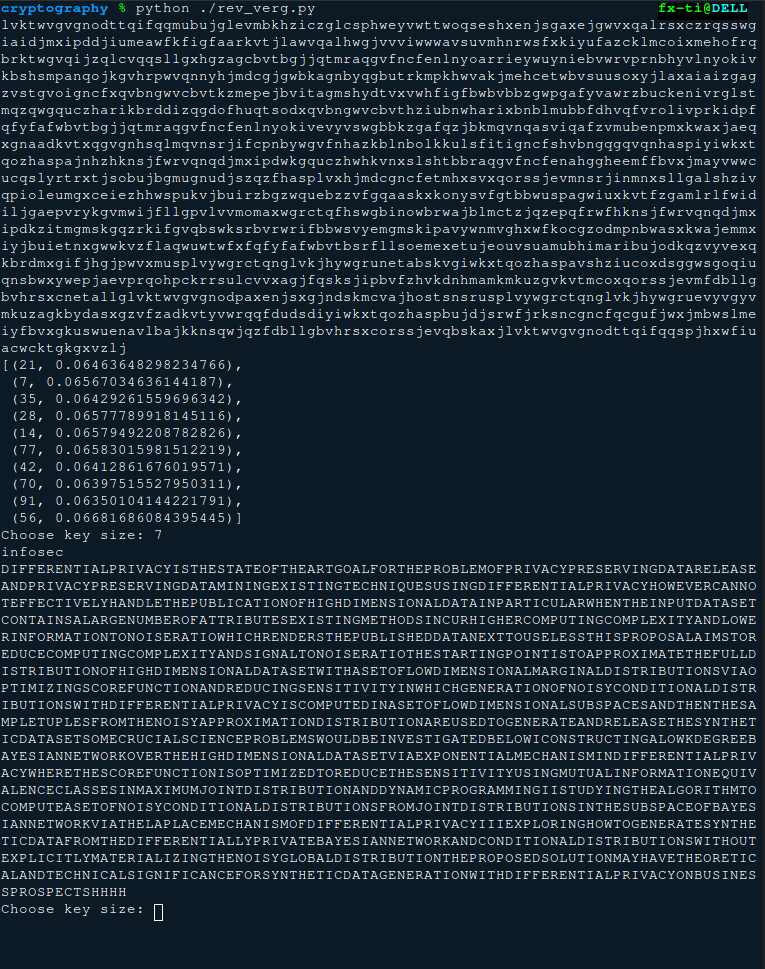
之后选取最可能的密钥长度，将密文按照所属的替换表分割，在各组上尝试所有可能偏移，取最符合统计规律的偏移将密文全部解密。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
while True:
    key_size = int(input("Choose key size: "))
    off = []
    for block in split(c, key_size):
        #print(block)
        alpha = dict()
        for z in range(26):
            alpha[chr(ord('A')+z)] = 0
        for x in block:
            alpha[x] += 1
        for k in alpha.keys():
            alpha[k] /= len(block)
        #statics is over
        ress = dict()
        for offset in range(1,26):
            acc = 0
            for k in alpha.keys():
                acc += alpha[k] * prob[chr(((ord(k) - ord('A') + offset) % 26) + ord('A'))]
            ress[offset] = acc
        pro = sorted(ress.items(), key=lambda a: abs(a[1] - 0.065))
        off.append(chr(26 - pro[0][0] + ord('a')))
        key = ''.join(off)
    print(key)
    print(''.join(dec(c, key)))

破解效果如下图：

给出脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
import math
import pprint

def enc(m, k):
    m = list(map(lambda x: (ord(x) - ord('A'), 'A') if 'A' <= x <= 'Z' else (ord(x) - ord('a'), 'a'), m))
    c = [chr(((m[i][0]+(ord(k[i%len(k)]) - ord('a')))%26) + ord(m[i][1])) for i in range(len(m))]
    return c

def dec(m, k):
    m = list(map(lambda x: (ord(x) - ord('A'), 'A') if 'A' <= x <= 'Z' else (ord(x) - ord('a'), 'a'), m))
    c = [chr(((m[i][0]-(ord(k[i%len(k)]) - ord('a'))+26)%26) + ord(m[i][1])) for i in range(len(m))]
    return c

prob = {
        'A': 0.082,
        'B': 0.015,
        'C': 0.028,
        'D': 0.043,
        'E': 0.127,
        'F': 0.022,
        'G': 0.02,
        'H': 0.061,
        'I': 0.07,
        'J': 0.002,
        'K': 0.008,
        'L': 0.04,
        'M': 0.024,
        'N': 0.067,
        'O': 0.075,
        'P': 0.019,
        'Q': 0.001,
        'R': 0.06,
        'S': 0.063,
        'T': 0.091,
        'U': 0.028,
        'V': 0.01,
        'W': 0.023,
        'X': 0.001,
        'Y': 0.02,
        'Z': 0.001,
        }

def split(c, i):
    c = list(c)
    return [list(map(lambda x: c[x], filter(lambda x: x % i == j, range(len(c))))) for j in range(i)]

c = input().upper()

res = dict()
#for i in range(1,len(c)):
for i in range(1,min(128, len(c))):
    tlist = []
    for tmp in split(c,i):
        alpha = dict()
        for z in range(26):
            alpha[chr(ord('A')+z)] = 0
        for x in tmp:
            alpha[x] += 1
        acc = 0
        for ke in alpha.keys():
            acc += alpha[ke] * (alpha[ke] - 1)
        if len(tmp) > 1:
            tlist.append(acc / (len(tmp) * (len(tmp) - 1)))
    #print(str(i) + " " + str(tlist))
    res[i] = sum(tlist) / len(tlist)

# 0.065

ss = sorted(res.items(), key=lambda a: abs(a[1] - 0.065))[:10]
pprint.pprint(ss)

while True:
    key_size = int(input("Choose key size: "))
    off = []
    for block in split(c, key_size):
        #print(block)
        alpha = dict()
        for z in range(26):
            alpha[chr(ord('A')+z)] = 0
        for x in block:
            alpha[x] += 1
        for k in alpha.keys():
            alpha[k] /= len(block)
        #statics is over
        ress = dict()
        for offset in range(1,26):
            acc = 0
            for k in alpha.keys():
                acc += alpha[k] * prob[chr(((ord(k) - ord('A') + offset) % 26) + ord('A'))]
            ress[offset] = acc
        pro = sorted(ress.items(), key=lambda a: abs(a[1] - 0.065))
        off.append(chr(26 - pro[0][0] + ord('a')))
        key = ''.join(off)
    print(key)
    print(''.join(dec(c, key)))

安全性分析

多表代换密码打破了原语言的字符出现规律，故其分析方法比单表代换密码复杂得多。多表代换密码对比单表代换密码安全性显著提高。但是仍然可以用一些统计分析法破解（具体参看上文攻击方法），但是前提是密文足够长。所以，较短的密文几乎是不可破译的。

流密码

RC4

RC4 是流密码的一种，突出优点是在软件中容易实现。它可能是世界上使用最广泛的流密码。RC4是WEP中采用的加密算法，也曾经是TLS可采用的算法之一。但在2015年，比利时鲁汶大学的研究人员Mathy Vanhoef及Frank Piessens，公布了针对RC4加密算法的新型攻击程式，可在75小时内取得cookie的内容。

算法实现

算法分为两个部分：

  1. 密钥调度算法：根据密钥打乱S盒顺序

  2. 伪随机生成算法：根据S盒输出伪随机数序列并更改S盒顺序

密钥调度算法

根据密钥打乱S盒顺序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void swap(unsigned char *a, unsigned char *b){
	unsigned char tmp = *a;
	*a = *b;
	*b = tmp;
}

void rc4_init(unsigned char *sbox, unsigned char *key, unsigned key_len){
	//sbox should be pointer to 256-bytes space
	unsigned char T[256] = {0};
	for(unsigned i = 0; i < 256; ++i){
		sbox[i] = i;
		T[i] = key[i % key_len];
	}

	unsigned j = 0;
	for(unsigned i = 0; i < 256; ++i){
		j = (j + sbox[i] + T[i]) % 256;
		swap(&sbox[i], &sbox[j]);
	}
}

伪随机生成算法

从 S 中随机抽取一个元素输出，并置换 S 以便下一次选取，选取的过程取决于索引 i 和 j ，产生的密文为异或的结果，所以我们在这步就顺便产生密文。

1
2
3
4
5
6
7
8
9
10
11
12
void rc4_prg(unsigned char *sbox, unsigned char *input, unsigned input_len){
	unsigned i = 0, j = 0;
	for(unsigned z = 0; z < input_len; ++z){
		//rc4 part starts
		i = (i + 1) % 256;
		j = (j + sbox[i]) % 256;
		swap(&sbox[i], &sbox[j]);
		unsigned c = sbox[(sbox[i] + sbox[j]) % 256];
		//rc4 part ends
		input[z] ^= c;
	}
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <stdio.h>
#include <string.h>

void swap(unsigned char *a, unsigned char *b){
	unsigned char tmp = *a;
	*a = *b;
	*b = tmp;
}

void rc4_init(unsigned char *sbox, unsigned char *key, unsigned key_len){
	//sbox should be pointer to 256-bytes space
	unsigned char T[256] = {0};
	for(unsigned i = 0; i < 256; ++i){
		sbox[i] = i;
		T[i] = key[i % key_len];
	}

	unsigned j = 0;
	for(unsigned i = 0; i < 256; ++i){
		j = (j + sbox[i] + T[i]) % 256;
		swap(&sbox[i], &sbox[j]);
	}
}

void rc4_prg(unsigned char *sbox, unsigned char *input, unsigned input_len){
	unsigned i = 0, j = 0;
	for(unsigned z = 0; z < input_len; ++z){
		//rc4 part starts
		i = (i + 1) % 256;
		j = (j + sbox[i]) % 256;
		swap(&sbox[i], &sbox[j]);
		unsigned c = sbox[(sbox[i] + sbox[j]) % 256];
		//rc4 part ends
		input[z] ^= c;
	}
}

void rc4(unsigned char *key, unsigned key_len, unsigned char *input, unsigned input_len){
	unsigned char sbox[256] = {0};
	rc4_init(sbox, key, key_len);
	rc4_prg(sbox, input, input_len);
}

int main(){
	unsigned char message[] = "123456";
	unsigned m_len = strlen((char *)message);
	unsigned char key[] = "123456";
	unsigned key_len = strlen((char *)key);
	rc4(key, key_len, message, m_len);
	for(unsigned i = 0; i < m_len; ++i)
		printf("%02x ", message[i]);
	rc4(key, key_len, message, m_len);
	puts(message);
	return 0;
}

运行结果

使用123456作为密钥对123456进行加密并解密还原：

正确性分析

因为加密解密用到的伪随机序列相同，而加密解密算法都是简单的异或运算，异或运算的逆运算仍然是异或运算，所以显然下式成立：$$RC4Decrypt(RC4Encrypt(m,k),k)=m$$

安全性

RC4 算法容易用软件实现，加解密速度快。需要特别注意的是，为保证安全强度，目前的 RC4 至少要求使用 128 位密钥。

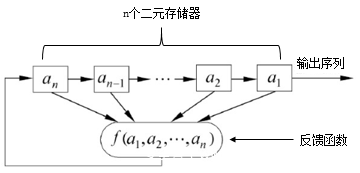
LFSR

LFSR全程线性反馈移位寄存器，是一种很典型的流密码，在嵌入式设备中经常被使用，因为其硬件实现的效率极高。

算法实现

如下：

其中的f函数：

对应的生成算法为：

1
2
3
4
5
6
7
8
9
10
uint64_t lfsr32(uint64_t *reg, uint64_t mask){
	uint64_t result = *reg & 0x1;
	uint64_t tmp = *reg & mask, lastbit = 0;
	while(tmp){
		tmp &= (tmp - 1);
		lastbit ^= 1;
	}
	*reg = (lastbit << (BITS - 1)) | (*reg >> 1);
	return result;
}

其中需要注意的是，LFSR寄存器中的状态空间受限于寄存器位数最大只能达到$2^n-1$，。而且这个最大情况依赖于mask的性质，所以是小于等于的关系。不过平时比赛中的bits均满足该性质，在已知mask的条件下进行解题，但由于之前出现的题目大都可以利用mask的高位得到唯一未知位高速破解，所以这里针对课本的m序列密码进行破译。

m序列密码的破译

在已知明文攻击下，假设破译者已经知道了2n位明密文对$M=m_1,m_2,…,m_{2n}$,$C=c1,c2,…,c_{2n}$，则可确定2n位长的密钥序列K。并由K推出反馈多项式的系数，从而确定该LFSR接下来的状态并得到余下的密钥序列。

首先由LFSR的计算过程可以得到方程组：

可以转换成矩阵求逆求解，以下为脚本使用SMT Solver求解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from z3 import *

# m = 0b011001111111001
# c = 0b101101011110011
# order = 5
# pls solve mask!

# first, calculate key sequence
m = 0b011001111111001
c = 0b101101011110011
k = m ^ c
k = list(map(int ,bin(k)[2:]))

# then, generate equations
order = 5
v = [BitVec('v%d'%i, 1) for i in range(order)]

s = Solver()

for i in range(5):
    Sum = 0
    for j in range(5):
        Sum ^= v[j] & k[i+j]
    s.add(k[5+i] == Sum)

print(s.check())
print(s.model())

可以得到正确的系数。

验证生成序列的周期

LFSR在抽头选用本原多项式时周期达到最大也即$2^n-1$，若要验证周期则随机选择一个非零的寄存器初始状态之后不断迭代检查寄存器是否还原了本来的初始状态。如果在重复之前所迭代的次数不够则说明周期比预期的要小。

整个验证过程中所花费时间最多的是迭代过程，分析一下LFSR的实现代码：

1
2
3
4
5
6
7
8
9
10
11
uint64_t lfsr32(uint64_t *reg, uint64_t mask){
	uint64_t result = *reg & 0x1;
	uint64_t tmp = *reg & mask, lastbit = 0;
    //loops here
	while(tmp){
		lastbit ^= tmp & 0x1;
		tmp >= 1;
	}
	*reg = (lastbit << (BITS - 1)) | (*reg >> 1);
	return result;
}

第一种优化

其中除了循环之外的操作都是常数时间内可以完成的，循环次数在这个写法下最差情况要循环$n-1$次。而优化之后代码如下：

1
2
3
4
5
6
7
8
9
10
uint64_t lfsr32(uint64_t *reg, uint64_t mask){
	uint64_t result = *reg & 0x1;
	uint64_t tmp = *reg & mask, lastbit = 0;
	while(tmp){
		tmp &= (tmp - 1);
		lastbit ^= 1;
	}
	*reg = (lastbit << (BITS - 1)) | (*reg >> 1);
	return result;
}

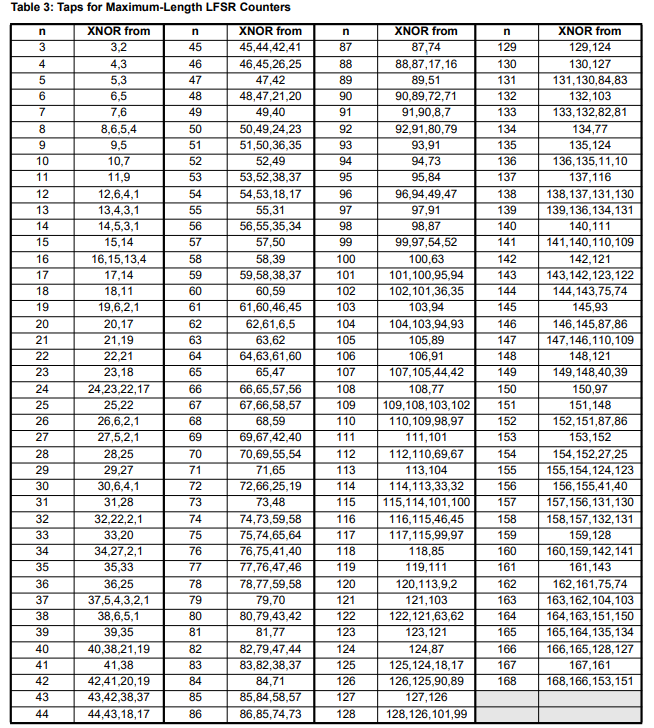
这个优化在于tmp &= (tmp - 1)这个过程，它保证能够去除tmp中从低位开始存在的第一个1。所以只需要循环tmp变量中1出现的次数次即可，检查Xilinx给出的LFSR规格手册可知从3位一直到168位LFSR均可选用4个及以下的抽头：

所以优化之后最差情况下循环次数为4。也即单轮循环中所消耗的时间比为$\frac{4t_{inner} + t_{left}}{(n-1)t_{inner}+t_{left}}$。

在16位LFSR的测试中取得了近一倍的加速，而且随着选用的寄存器位数上升，加速效果越好。

第二种优化

同时还提出另一种优化方法，利用分治的思想在比特位操作层面实现tmp中所有位的相互亦或：

1
2
3
4
5
6
7
8
9
10
11
12
uint64_t lfsr32(uint64_t *reg, uint64_t mask){
	uint64_t result = *reg & 0x1;
	uint64_t tmp = *reg & mask, lastbit = 0;
	lastbit = (tmp & 0x5555555555555555) ^ ((tmp >> 1) & 0x5555555555555555);
	lastbit = (lastbit & 0x3333333333333333) ^ ((lastbit >> 2) & 0x3333333333333333);
	lastbit = (lastbit & 0x0F0F0F0F0F0F0F0F) ^ ((lastbit >> 4) & 0x0F0F0F0F0F0F0F0F);
	lastbit = (lastbit & 0x00FF00FF00FF00FF) ^ ((lastbit >> 8) & 0x00FF00FF00FF00FF);
	lastbit = (lastbit & 0x0000FFFF0000FFFF) ^ ((lastbit >> 16)& 0x0000FFFF0000FFFF);
	lastbit = (lastbit & 0x00000000FFFFFFFF) ^ ((lastbit >> 32)& 0x00000000FFFFFFFF);
	*reg = (lastbit << (BITS - 1)) | (*reg >> 1);
	return result;
}

该方法利用分治法枚举完了所有位互相亦或的结果，所花时间固定为$log_2{n}t_{inner} + t_{left}$，其中$n$为LFSR寄存器位数。在对于$log_2{n} > 4$，也即16位LFSR之后应该体现不出性能优势。然而该种优化完全省去了循环中判断的过程，而对于现代处理器而言在不出现分支判断的情况下可以充分利用流水线。所以相较于上一种优化后仍存在循环处分支判断的方案，性能出现差距的位数被后移，直到42位差距才达到0.5秒且可反复测量。

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;

#define ONE (1ULL)
#define BITS (42)

uint64_t lfsr32(uint64_t *reg, uint64_t mask){
	uint64_t result = *reg & 0x1;
	uint64_t tmp = *reg & mask, lastbit = 0;
	while(tmp){
		tmp &= (tmp - 1);
		lastbit ^= 1;
	}
	*reg = (lastbit << (BITS - 1)) | (*reg >> 1);
	return result;
}


int main(){
	//unsigned MASK = (1 << 22) | (1 << 17); //x^32 + x^22 + x^2 + x^1 + 1
	uint64_t MASK = (ONE << 41) | (ONE << 39) | (ONE << 36) | (ONE << 34); 
	//https://www.partow.net/programming/polynomials/index.html#deg31
	//https://web.archive.org/web/20161007061934/http://courses.cse.tamu.edu/csce680/walker/lfsr_table.pdf
	const uint64_t INIT_REG = ONE;
	uint64_t REG = INIT_REG;

	uint64_t i = 0;

	uint64_t upper = ONE << BITS;

	for(; i < upper; ++i){
		uint64_t r = lfsr32(&REG, MASK);
		if(INIT_REG == REG)
			break;

		if(i % (upper >> 7) == 0)
			printf("%.3lf \n", 100.0*i / upper);
	}
	if(i == upper)
		cout << i << ", right" << endl;
	else
		cout << i << ", wrong" << endl;

	return 0;
}

运行结果

第一种优化

…

96.88

98.44

4398046511104, right

./lfsr 1413.45s user 0.01s system 99% cpu 23:34.82 total

第二种优化

…

96.88

98.44

4398046511104, right

./lfsr 1414.00s user 0.01s system 99% cpu 23:35.82 total

安全性分析

LFSR的软件实现的性能在适当优化后很强，同时硬件实现几乎可以说是最快的。LFSR在选取正确的抽头并使用随机的初始寄存器状态时，生成的密钥会遍历整个$2^n-1$的空间。只要密钥序列不被泄露就很安全，所以要想办法避免攻击者取得明文-密文对，否则在得到足够长的密钥序列之后LFSR便不再安全。

分组密码

DES

DES(Data Encryption Standard)是密码学历史上第一个广泛应用于商用数据保密的密码算法，并开创了公开密码算法的先例，极大地促进了密码学的发展。它分组长度 64 比特，密钥长度 64 比特（其中有效长度为 56 比特），8 的倍数位为奇校验位（保证每 8 位有奇数个 1）。

算法实现

密钥编排算法

用于生成迭代的子密钥。具体过程为：

64位初始密钥经过置换选择1 ( PC-1 ) 后变成 56 位，经过循环左移和置换选择2 ( PC-2 ) 后分别得到 16 个 48 位子密钥 Ki用做每一轮的迭代运算。

置换选择1

1
2
3
4
5
6
7
8
//Do the intial permutation for key
tmp = 0;
for(unsigned i = 0; i < 56; ++i){
	tmp <<= 1;
	tmp |= (k >> (64 - PC1[i])) & 0x1;
}
C = (tmp >> 28) & 0xfffffff;
D = tmp & 0xfffffff;

循环左移

1
2
3
4
5
for(unsigned j = 0; j < key_shift[i]; ++j){
	C = ((C << 1) & 0x0fffffff) | ((C >> 27) & 0x1);
	D = ((D << 1) & 0x0fffffff) | ((D >> 27) & 0x1);
}
tmp = (C << 28) | (D);

F函数

也称轮函数，包括四个过程：

  1. 扩展置换 ( E 盒 )

    通过扩展置换，数据的右半部分 Ri 从 32 位扩展到 48 位。扩展置换改变了位的次序，重复了某些位。

    1
    2
    3
    4
    5
    tmp = 0;
    for(unsigned j = 0; j < 48; ++j){
    	tmp <<= 1;
    	tmp |= (R >> (32 - ebox[j])) & 0x1;
    }

  2. 密钥加

    E 盒输出与子密钥 Xor （逐位异或）。

    1
    2
    3
    4
    if(mode == ENCRYPT)
    	tmp ^= key_list[i];
    else
    	tmp ^= key_list[15 - i];

  3. S 盒

    实现非线性代换，是查表运算，8 个 S 盒对应把 48 位分成 8 个组（6 位一组）。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    //Third, subtitle it with sbox
    s_result = 0;
    for(unsigned j = 0; j < 8; ++j){
    	tmp2 = ((tmp & (0xfc0000000000 >> (6 * j))) >> (42 - 6 * j));
    	uint8 row = ((tmp2 >> 4) & 0x2) | (tmp2 & 0x1);
    	uint8 column = (tmp2 & 0x1e) >> 1;
    	s_result <<= 4;
    	s_result |= sbox[j][row * 16 + column];
    }

  4. P 盒

    1
    2
    3
    4
    5
    6
    //Fourth, replace operation
    p_result = 0;
    for(unsigned j = 0; j < 32; ++j){
    	p_result <<= 1;
    	p_result |= (s_result >> (32 - pbox[j])) & 0x1;
    }

完整代码

省略替换表的数据，太多了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
#include <stdio.h>

//For standard x86-64 machine around 2020
typedef unsigned long long uint64;
typedef unsigned int uint32;
typedef unsigned char uint8;

uint8 sbox[8][4 * 16] = {
	...
};

uint8 ebox[48] = {
	...
};

uint8 pbox[32] = {
	...
};

uint8 m_IP[64] = {
	...
};

uint8 m_PI[64] = {
	...
};

uint8 PC1[64] = {
	...
};

uint8 PC2[48] = {
	14, 17, 11, 24,  1,  5,
     3, 28, 15,  6, 21, 10,
    23, 19, 12,  4, 26,  8,
    16,  7, 27, 20, 13,  2,
    41, 52, 31, 37, 47, 55,
    30, 40, 51, 45, 33, 48,
    44, 49, 39, 56, 34, 53,
    46, 42, 50, 36, 29, 32
};

uint8 key_shift[16] = {
 /* 1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16 */
    1,  1,  2,  2,  2,  2,  2,  2,  1,  2,  2,  2,  2,  2,  2,  1
};

enum MODE {
	ENCRYPT,
	DECRYPT,
};

uint64 des(uint64 message, uint64 key, int mode){
	uint64 m = 0, k = 0, tmp, tmp2, L, R, C, D;
	uint64 key_list[16] = {0};
	uint64 s_result, p_result;
	m = message;
	k = key;
//uint64 des(uint8 *message, uint8 *key, int mode){
	/*
	//copy message from char array to one unsigned 64-bits var
	for(unsigned i = 0; i < 8; ++i){
		m <<= 8;
		m |= message[i];
	}

	//copy key from char array to one unsigned 64-bits var
	for(unsigned i = 0; i < 8; ++i){
		k <<= 8;
		k |= key[i];
	}
	*/

	//Do the initial permutation for message
	tmp = 0;
	for(unsigned i = 0; i < 64; ++i){
		tmp <<= 1;
		tmp |= (m >> (64 - m_IP[i])) & 0x1;
	}
	L = (tmp >> 32) & 0xffffffff;
	R = tmp & 0xffffffff;

	//Do the intial permutation for key
	tmp = 0;
	for(unsigned i = 0; i < 56; ++i){
		tmp <<= 1;
		tmp |= (k >> (64 - PC1[i])) & 0x1;
	}
	C = (tmp >> 28) & 0xfffffff;
	D = tmp & 0xfffffff;

	//Prepare all the keys for encryption precedure
	//Fill the key_list for following 16 round operations
	for(unsigned i = 0; i < 16; ++i){
		for(unsigned j = 0; j < key_shift[i]; ++j){
			C = ((C << 1) & 0x0fffffff) | ((C >> 27) & 0x1);
			D = ((D << 1) & 0x0fffffff) | ((D >> 27) & 0x1);
		}
		tmp = (C << 28) | (D);

		key_list[i] = 0;
		for(unsigned j = 0; j < 48; ++j){
			key_list[i] <<= 1;
			key_list[i] |= (tmp >> (56 - PC2[j])) & 0x1;
		}
	}

	//Begin encryption rounds
	for(unsigned i = 0; i < 16; ++i){
		//F funtion start
		//First, extend R part
		tmp = 0;
		for(unsigned j = 0; j < 48; ++j){
			tmp <<= 1;
			tmp |= (R >> (32 - ebox[j])) & 0x1;
		}
		//Second, xor it with key
		if(mode == ENCRYPT)
			tmp ^= key_list[i];
		else
			tmp ^= key_list[15 - i];
		//Third, subtitle it with sbox
		s_result = 0;
		for(unsigned j = 0; j < 8; ++j){
			tmp2 = ((tmp & (0xfc0000000000 >> (6 * j))) >> (42 - 6 * j));
			uint8 row = ((tmp2 >> 4) & 0x2) | (tmp2 & 0x1);
			uint8 column = (tmp2 & 0x1e) >> 1;
			s_result <<= 4;
			s_result |= sbox[j][row * 16 + column];
		}
		//Fourth, replace operation
		p_result = 0;
		for(unsigned j = 0; j < 32; ++j){
			p_result <<= 1;
			p_result |= (s_result >> (32 - pbox[j])) & 0x1;
		}

		tmp = R;
		R = L ^ p_result;
		L = tmp;
	}
	//Combine L and R to get result
	tmp = (R << 32) | L;
	//Inverse the initial permuation
	tmp2 = 0;
	for(unsigned i = 0; i < 64; ++i){
		tmp2 <<= 1;
		tmp2 |= (tmp >> (64 - m_PI[i])) & 0x1;
	}
	return tmp2;
}

int main(){
	uint64 m = 0x02468aceeca86420;
	uint64 k = 0x0f1571c947d9e859;
	uint64 res = m;
    for (unsigned i = 0; i < 16; i++) {
    	if (i%2 == 0) {
        	res = des(res, res, ENCRYPT);
        	printf ("E: %016llx\n", res);
    	} else {
        	res = des(res, res, DECRYPT);
        	printf ("D: %016llx\n", res);
    	}
    }
    res = des(m, k, ENCRYPT);
    printf ("E: %016llx\n", res);

    res = des(res, k, DECRYPT);
    printf ("D: %016llx\n", res);
	return 0;
}

运行结果：

正确性分析

解密过程实际上就是加密过程的逆过程，在加密中，密钥编排算法中的循环移位是循环左移，则在解密中，使用循环右移，致使加密过程中每轮子密钥和解密过程中每轮子密钥顺序刚好相反。加密和解密过程满足：

$DESDecrypt(DESEncrypt(M))=M$

安全性分析

弱密钥

存在使得加密算法和解密算法没有区别的密钥。即有：$Ek(Ek(M))=Dk(Dk(M))=M$

这种密钥使得密钥编排算法中，CC 和 DD始终不变（全0或全1）。相应的，还有半弱密钥。

互补性

若$ c=Ek(m)$则 $\overline{c}=E_{\overline{e}}(\overline{m})$，这使得在选择明文攻击下所需的工作量减半（从 $2^{56}$ 减少到 $2^{55}$ ）。

故而对于DES，现代一般选用3DES也即利用多重DES过程来进行加密，应用很广泛。

AES

AES(Advanced Encryption Standard)是用来替换DES的加密算法标准，要求性能不低于3DES，安全性比3DES强，而且在世界范围内是可以免费获得的。它的分组长度为128位，而密钥长度可变，分别为：128，192或256位。加密轮数也有所不同，这里以AES128为准。

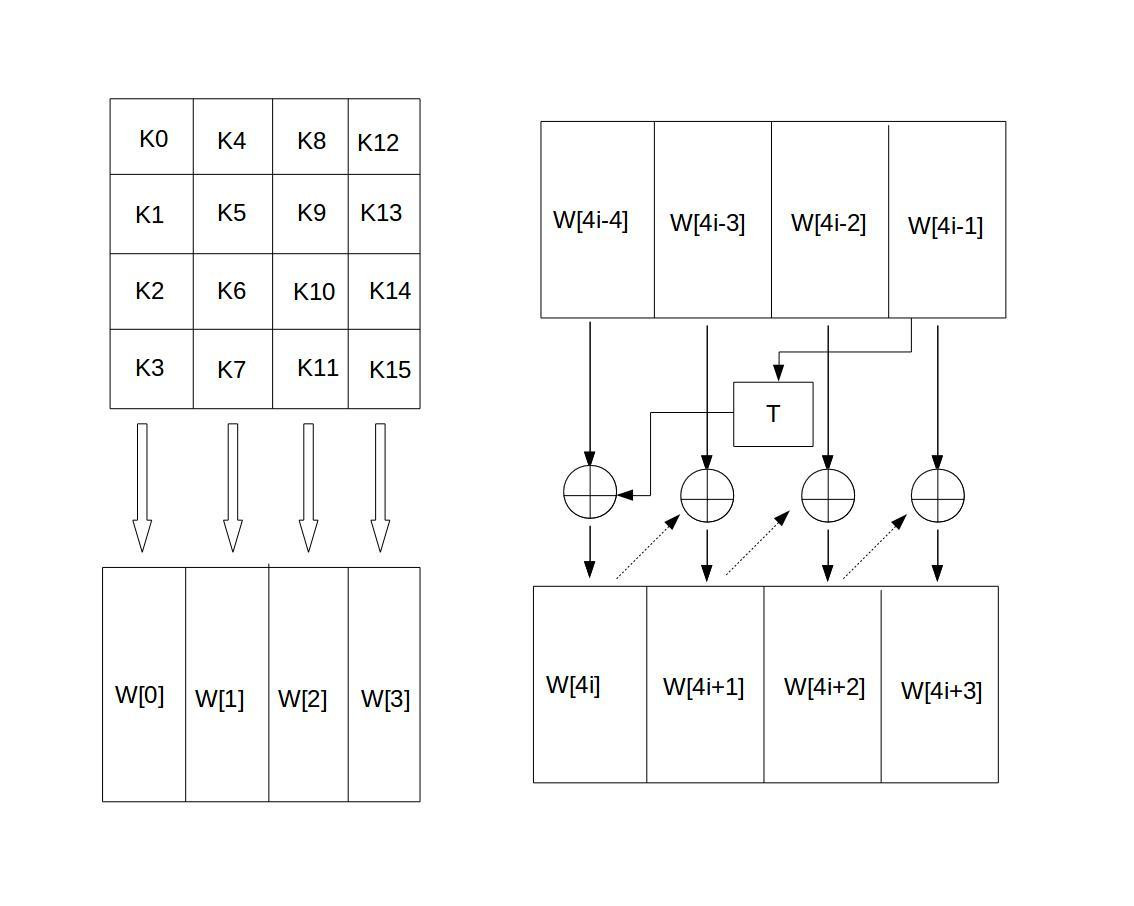
算法实现

密钥拓展算法

用于生成迭代的子密钥。具体过程为：

将128位密钥装入4x4矩阵中，然后通过递归过程对矩阵进行拓展得到10个4x4矩阵。

如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void keyExpansion(uint8 *key, uint8 keyed[][4][4]){
	for(unsigned i = 0; i < 4; ++i)
		for(unsigned j = 0; j < 4; ++j)
			keyed[0][j][i] = key[i * 4 + j];
	for(unsigned i = 1; i <= 10; ++i){
		for(unsigned j = 0; j < 4; ++j){
			if(j == 0){
				for(unsigned z = 0; z < 4; ++z)
					keyed[i][z][j] = sbox[keyed[i-1][(z + 1) % 4][3]];
				keyed[i][0][j] ^= Rcon[i - 1];
			} else {
				for(unsigned z = 0; z < 4; ++z)
					keyed[i][z][j] = keyed[i][z][j-1];
			}
			for(unsigned z = 0; z < 4; ++z)
				keyed[i][z][j] ^= keyed[i - 1][z][j];
		}
	}
}

字节代换

1
2
3
4
5
6
7
8
9
10
void byteSubtitle(uint8 *m, uint8 *box){
	for(unsigned i = 0; i < 16; ++i){
		/*
		unsigned row = m[i] >> 4;
		unsigned column = m[i] & 0xf;
		m[i] = box[row * 16 + column];
		*/
		m[i] = box[m[i]];
	}
}

行移位

1
2
3
4
5
6
7
8
9
10
void byteSubtitle(uint8 *m, uint8 *box){
	for(unsigned i = 0; i < 16; ++i){
		/*
		unsigned row = m[i] >> 4;
		unsigned column = m[i] & 0xf;
		m[i] = box[row * 16 + column];
		*/
		m[i] = box[m[i]];
	}
}

列混淆

1
2
3
4
5
6
7
8
9
10
11
12
void columnMix(uint8 *v){
	uint8 tmp[4] = {0};
	for(unsigned i = 0; i < 4; ++i){
		for(unsigned j = 0; j < 4; ++j)
			tmp[j] = v[j * 4 + i];
		for(unsigned j = 0; j < 4; ++j)
			v[j * 4 + i] = gf2_8_multiply(mix_matrix[j][0], tmp[0]) ^
						gf2_8_multiply(mix_matrix[j][1], tmp[1]) ^
						gf2_8_multiply(mix_matrix[j][2], tmp[2]) ^
						gf2_8_multiply(mix_matrix[j][3], tmp[3]);
	}
}

其中的gf2_8_multiply是在基于$GF(2^8)$上的二元运算，实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
uint8 gf2_8_multiply(uint8 a, uint8 b){
	uint8 acc = b, res = (a & 0x1) ? b : 0;
	a >>= 1;
	while(a){
		if(acc & 0x80)
			acc = (acc << 1) ^ 0x1b;
		else 
			acc <<= 1;
		if(a & 0x1)
			res ^= acc;
		a >>= 1;
	}
	return res;
}

计算过程即是利用如下结论：

轮密钥加

过程即是简单的xor

1
2
3
4
5
6
7
void Xor(uint8 *xored, uint8 *xorer){
	for(unsigned i = 0; i < 16; ++i)
		xored[i] ^= xorer[i];
}void Xor(uint8 *xored, uint8 *xorer){
	for(unsigned i = 0; i < 16; ++i)
		xored[i] ^= xorer[i];
}

完整代码

省略替换表的数据，太多了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
#include <stdio.h>

//For standard x86-64 machine around 2020
typedef unsigned long long uint64;
typedef unsigned int uint32;
typedef unsigned char uint8;

uint8 sbox[256] = {
	...
};

uint8 invsbox[256] = {
	...
};

void byteSubtitle(uint8 *m, uint8 *box){
	for(unsigned i = 0; i < 16; ++i){
		/*
		unsigned row = m[i] >> 4;
		unsigned column = m[i] & 0xf;
		m[i] = box[row * 16 + column];
		*/
		m[i] = box[m[i]];
	}
}

void shiftRow(uint8 *v){
	uint8 tmp[4];
	for(unsigned i = 0; i < 4; ++i){
		for(unsigned j = 0; j < 4; ++j)
			tmp[j] = v[i * 4 + ((j + i) % 4)];
		for(unsigned j = 0; j < 4; ++j)
			v[i * 4 + j] = tmp[j];
	}
}

void invShiftRow(uint8 *v){
	uint8 tmp[4];
	for(unsigned i = 0; i < 4; ++i){
		for(unsigned j = 0; j < 4; ++j)
			tmp[j] = v[i * 4 + ((j - i + 4) % 4)];
		for(unsigned j = 0; j < 4; ++j)
			v[i * 4 + j] = tmp[j];
	}
}

uint8 mix_matrix[4][4] = {
	{2, 3, 1, 1},
	{1, 2, 3, 1},
	{1, 1, 2, 3},
	{3, 1, 1, 2},
};

uint8 inv_mix_matrix[4][4] = {
	{0xe, 0xb, 0xd, 0x9},
	{0x9, 0xe, 0xb, 0xd},
	{0xd, 0x9, 0xe, 0xb},
	{0xb, 0xd, 0x9, 0xe},
};

uint8 gf2_8_multiply(uint8 a, uint8 b){
	uint8 acc = b, res = (a & 0x1) ? b : 0;
	a >>= 1;
	while(a){
		if(acc & 0x80)
			acc = (acc << 1) ^ 0x1b;
		else 
			acc <<= 1;
		if(a & 0x1)
			res ^= acc;
		a >>= 1;
	}
	return res;
}

void columnMix(uint8 *v){
	uint8 tmp[4] = {0};
	for(unsigned i = 0; i < 4; ++i){
		for(unsigned j = 0; j < 4; ++j)
			tmp[j] = v[j * 4 + i];
		for(unsigned j = 0; j < 4; ++j)
			v[j * 4 + i] = gf2_8_multiply(mix_matrix[j][0], tmp[0]) ^
						gf2_8_multiply(mix_matrix[j][1], tmp[1]) ^
						gf2_8_multiply(mix_matrix[j][2], tmp[2]) ^
						gf2_8_multiply(mix_matrix[j][3], tmp[3]);
	}
}

void invColumnMix(uint8 *v){
	uint8 tmp[4] = {0};
	for(unsigned i = 0; i < 4; ++i){
		for(unsigned j = 0; j < 4; ++j)
			tmp[j] = v[j * 4 + i];
		for(unsigned j = 0; j < 4; ++j)
			v[j * 4 + i] = gf2_8_multiply(inv_mix_matrix[j][0], tmp[0]) ^
						gf2_8_multiply(inv_mix_matrix[j][1], tmp[1]) ^
						gf2_8_multiply(inv_mix_matrix[j][2], tmp[2]) ^
						gf2_8_multiply(inv_mix_matrix[j][3], tmp[3]);
	}
}

void Xor(uint8 *xored, uint8 *xorer){
	for(unsigned i = 0; i < 16; ++i)
		xored[i] ^= xorer[i];
}

uint8 Rcon[10] = {0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36};

void keyExpansion(uint8 *key, uint8 keyed[][4][4]){
	for(unsigned i = 0; i < 4; ++i)
		for(unsigned j = 0; j < 4; ++j)
			keyed[0][j][i] = key[i * 4 + j];
	for(unsigned i = 1; i <= 10; ++i){
		for(unsigned j = 0; j < 4; ++j){
			if(j == 0){
				for(unsigned z = 0; z < 4; ++z)
					keyed[i][z][j] = sbox[keyed[i-1][(z + 1) % 4][3]];
				keyed[i][0][j] ^= Rcon[i - 1];
			} else {
				for(unsigned z = 0; z < 4; ++z)
					keyed[i][z][j] = keyed[i][z][j-1];
			}
			for(unsigned z = 0; z < 4; ++z)
				keyed[i][z][j] ^= keyed[i - 1][z][j];
		}
	}
}

void aes_encrypt(uint8 *m, uint8 *key){
	uint8 state[4][4] = {{0}};
	for(unsigned i = 0; i < 4; ++i)
		for(unsigned j = 0; j < 4; ++j)
			state[i][j] = m[j * 4 + i];

	uint8 keyed[11][4][4] = {{{0}}};
	keyExpansion(key, keyed);

	Xor((uint8 *)state, (uint8 *)keyed[0]);

	for(unsigned i = 1; i <= 10; ++i){
		byteSubtitle((uint8 *)state, sbox);
		shiftRow((uint8 *)state);
		if(i != 10)
			columnMix((uint8 *)state);
		Xor((uint8 *)state, (uint8 *)keyed[i]);
	}

	for(unsigned i = 0; i < 4; ++i)
		for(unsigned j = 0; j < 4; ++j)
			m[j * 4 + i] = state[i][j];
}

void aes_decrypt(uint8 *c, uint8 *key){
	uint8 state[4][4] = {{0}};
	for(unsigned i = 0; i < 4; ++i)
		for(unsigned j = 0; j < 4; ++j)
			state[i][j] = c[j * 4 + i];

	uint8 keyed[11][4][4] = {{{0}}};
	keyExpansion(key, keyed);

	Xor((uint8 *)state, (uint8 *)keyed[10]);

	for(int i = 9; i >= 0; --i){
		invShiftRow((uint8 *)state);
		byteSubtitle((uint8 *)state, invsbox);
		Xor((uint8 *)state, (uint8 *)keyed[i]);
		if(i)
			invColumnMix((uint8 *)state);
	}

	for(unsigned i = 0; i < 4; ++i)
		for(unsigned j = 0; j < 4; ++j)
			c[j * 4 + i] = state[i][j];
}

int main(){
	uint8 key[16] = {
		0x00, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07,
		0x08, 0x09, 0x0a, 0x0b, 0x0c, 0x0d, 0x0e, 0x0f,
	};
	uint8 message[16] = {
		0x00, 0x11, 0x22, 0x33, 0x44, 0x55, 0x66, 0x77,
		0x88, 0x99, 0xaa, 0xbb, 0xcc, 0xdd, 0xee, 0xff,
	};
	aes_encrypt(message, key);
	for(unsigned i = 0; i < 16; ++i)
		printf("%02x ", message[i]);
	printf("\n");
	aes_decrypt(message, key);
	for(unsigned i = 0; i < 16; ++i)
		printf("%02x ", message[i]);
	printf("\n");
	return 0;
}

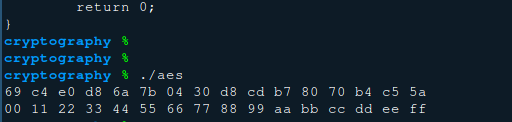
运行结果：

正确性分析

解密过程实际上就是加密过程的逆过程，加密和解密过程满足：

$AESDecrypt(AESEncrypt(M))=M$

安全性分析

AES表现出足够的安全性，没有已知的攻击方法能攻击AES，同时AES所采用的实现方法非常利于防止能量攻击和计时攻击。

公钥密码

RSA

RSA的安全性基于大整数分解的困难性。过程如下：

  1. 选取两个安全大素数p和q(至少1024比特)。
  2. 计算乘积$n = p \times q$， $\phi(n) = (p - 1)(q - 1)$，其中$\phi(n)$为$n$的欧拉函数。
  3. 随机选择整数$e(1 < e < \phi(e)), gcd(e, \phi(n)) = 1$，作为公钥
  4. 计算私钥$d \equiv e^{-1} (mod \phi(n))$

而加密过程是$c \equiv m^e (mod n)$

解密过程是$m \equiv c^d(mod n)$

算法实现

大素数生成

Miler-Rabin 算法

Miller-Rabin 算法常用来判断一个大整数是否是素数，如果该算法判定一个数是合数，则这个数肯定是合数。Miller-Rabin 算法是一个概率算法，也就是说，若该算法判定一个大整数是素数，则该整数不是素数的概率很小。

Miller-Rabin 概率检测算法的理论基础是费马小定理,即设 n 是正奇整数，如果 n 是素数，则对于任意整数$b (1 < b < n-1)$，有$b^{n-1}≡1(mod n)$。该命题的逆命题为：若$b^{n-1}\equiv1(mod n)$不成立，则n是合数。但该命题的逆命题并不一定成立。即若$b^{n-1}\equiv1(mod n)$，n 可能是素数，也可能是合数。

简单来说，如果对整数$b (1 < b < n-1),（n, b）= 1$，使得$b^{n-1}\equiv1(mod n)$不成立，则 n 是合数，如果成立，则 n 可能是素数，也可能是合数，需要通过再找别的整数$b (1 < b < n-1)$，进行判断，只要有一种b不成立则为合数（注意可能两个字）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import random

def gcd(a, b):
    while b != 0:
        a, b = b, a%b
    return a

def MilerTest(n, testTimes = 80):
    if n % 2 == 0:
        return False
    for _ in range(testTimes):
        tmp = random.randrange(1, n)
        if gcd(tmp, n) != 1:
            return False
        if pow(tmp, n-1, n) != 1:
            return False 
    return True

其中testTimes为测试次数，次数越多，n为素数的概率越大，权衡之后根据网上所说设定为80.

加密过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import *
import gmpy2

p = getPrime(2048)
q = getPrime(2048)
n = p * q
phi_n = (p - 1) * (q - 1)
e = 65537

d = gmpy2.invert(e ,phi_n)

m = bytes_to_long(raw_input())
c = pow(m, e, n)
print(c)

解密过程

1
2
3
4
5
from Crypto.Util.number import *
import gmpy2

c = pow(m, e, n)
print(c)

攻击方法

低加密指数攻击

为了使加密高效，一般希望选取较小的加密指数 e ，但是 e 不能太小，否则容易遭到低加密指数攻击。

假设用户使用的密钥e = 3 。考虑到加密关系满足：$c \equiv m^3 (mod n)$

则有: $m^3 =c + k * n$

则: $m = \sqrt[3]{c+k*n}$

攻击者可以从小到大枚举 k ，依次开三次根，直到开出整数为止。

低加密指数广播攻击

还有一种情况是如果给 k 个用户发的都是同个低加密指数比如 e=3，在不同的模数 n1.n2,n3下 ，可由 CRT（中国剩余定理） 解出$m^3$，从而直接开三次根解出 m，比赛考了很多次了。

效率分析

RSA基于大数分解问题，必然涉及大量的大数运算，故而效率比对称密码如DES，AES要低。在实现上Miler-Rabin所消耗的时间不确定。同时加密和解密中常用的pow函数通过优化之后即使时间复杂度为$O(log_2(min(a, b)))$，但是其中的计算依旧是大数运算，很耗时间。

非对称加密算法中 1024 bit 密钥的强度相当于对称加密算法 80bit 密钥的强度。但是，从效率上，密钥长度增长一倍，公钥操作所需时间增加约 4 倍，私钥操作所需时间增加约 8 倍，公私钥生成时间约增长16倍。

安全性分析

RSA 基于大数因数分解的困难性，前人已经提出了二次筛因子分解法、椭圆曲线因子分解法、数域筛因子分解法等。但是，因数分解的复杂性并没有降到多项式水平，所以短时间内仍无法破译。当大整数因数分解难题被攻破或量子计算机普及之日，RSA 将不再安全。

现今采用RSA的系统被攻破往往是因为不当的使用方法，不如密钥过短，e过小这种情况。所以在使用时要经过严格的安全审计，或者使用成熟并验证过的现有实现来规避危险。

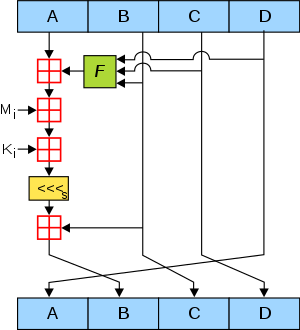
哈希函数

MD5

MD5由美国麻省理工学院的Rivest设计，该算法接受长度小于$2^{64}$比特的消息，输出长度为128比特的信息摘要。

算法实现

要注意MD5的上下文规定了是小端序，所以给出两个函数方便进行转换：

1
2
3
4
5
6
7
8
9
10
11
12
13
void to_bytes(uint8 *v, uint32 val){
	v[0] = (uint8)val & 0xff;
	v[1] = (uint8)(val >> 8) & 0xff;
	v[2] = (uint8)(val >> 16) & 0xff;
	v[3] = (uint8)(val >> 24) & 0xff;
}

uint32 to_uint32(uint8 *bytes){
	return (uint32)bytes[0] | 
			(((uint32)bytes[1]) << 8) |
			(((uint32)bytes[2]) << 16) |
			(((uint32)bytes[3]) << 24);
}

Padding

首先对于输入进行填充，满足长度模512与448同余，为的是提供64的空间用来存储消息的实际长度。

1
2
3
4
5
6
7
8
9
10
11
unsigned new_len;
for(new_len = len + 1; new_len % (512 / 8) != 448 / 8; ++new_len) {}

uint8 *msg = (uint8 *)malloc(sizeof(uint8) * (new_len + 8));
memcpy(msg, m, len);
msg[len] = 0x80;
for(unsigned i = len + 1; i < new_len; ++i)
	msg[i] = 0;

to_bytes(&msg[new_len], len * 8);
to_bytes(&msg[new_len + 4], len >> 29); // >> 32 * 8

初始化链接变量

1
2
3
4
uint32 A = 0x67452301;
uint32 B = 0xefcdab89;
uint32 C = 0x98badcfe;
uint32 D = 0x10325476;

这里的变量看起来和课本上的不一样，实际上是经过了to_bytes函数完成小端序转换之后。

循环过程

每一步中完成上图的操作，可以得到：变量D赋给变量A，变量B赋给变量C，变量C赋给变量D，而变量B由变量A与非线性函数结果相加，再与Mi，Ki相加，最后循环左移s位与B相加所得。

非线性函数如下：

在C中用宏完成定义

1
2
3
4
#define F(X, Y, Z) (((X) & (Y)) | (~(X) & (Z)))
#define G(X, Y, Z) (((X) & (Z)) | ((Y) & ~(Z)))
#define H(X, Y, Z) ((X) ^ (Y) ^ (Z))
#define I(X, Y, Z) ((Y) ^ ((X) | ~(Z)))

Mi是来自消息的32bit子分组，Ki是一个伪随机的常数，用来消除输入数据的规律性。

而循环左移次数由MD5算法所规定，左移过程同样用宏定义

1
#define LROTATE(x, n) (((x) << (n)) | ((x) >> (32 - (n))))

完成全部迭代之后根据小端序还原即可得到结果

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

//For standard x86-64 machine around 2020
typedef unsigned long long uint64;
typedef unsigned int uint32;
typedef unsigned char uint8;

#define F(X, Y, Z) (((X) & (Y)) | (~(X) & (Z)))
#define G(X, Y, Z) (((X) & (Z)) | ((Y) & ~(Z)))
#define H(X, Y, Z) ((X) ^ (Y) ^ (Z))
#define I(X, Y, Z) ((Y) ^ ((X) | ~(Z)))
#define LROTATE(x, n) (((x) << (n)) | ((x) >> (32 - (n))))

uint32 t[64] = {
	0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee,
	0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501,
	0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be,
	0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821,
	0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa,
	0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
	0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed,
	0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a,
	0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c,
	0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
	0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05,
	0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
	0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039,
	0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1,
	0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1,
	0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391
};

uint32 s[] = {
	7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22,
	5,  9, 14, 20, 5,  9, 14, 20, 5,  9, 14, 20, 5,  9, 14, 20,
	4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23,
	6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21
};

void to_bytes(uint8 *v, uint32 val){
	v[0] = (uint8)val & 0xff;
	v[1] = (uint8)(val >> 8) & 0xff;
	v[2] = (uint8)(val >> 16) & 0xff;
	v[3] = (uint8)(val >> 24) & 0xff;
}

uint32 to_uint32(uint8 *bytes){
	return (uint32)bytes[0] | 
			(((uint32)bytes[1]) << 8) |
			(((uint32)bytes[2]) << 16) |
			(((uint32)bytes[3]) << 24);
}

void md5(uint8 *m, unsigned len, uint8 *hash){
	uint32 A = 0x67452301;
	uint32 B = 0xefcdab89;
	uint32 C = 0x98badcfe;
	uint32 D = 0x10325476;

	unsigned new_len;
	for(new_len = len + 1; new_len % (512 / 8) != 448 / 8; ++new_len) {}

	uint8 *msg = (uint8 *)malloc(sizeof(uint8) * (new_len + 8));
	memcpy(msg, m, len);
	msg[len] = 0x80;
	for(unsigned i = len + 1; i < new_len; ++i)
		msg[i] = 0;

	to_bytes(&msg[new_len], len * 8);
	to_bytes(&msg[new_len + 4], len >> 29); // >> 32 * 8

	for(unsigned i = 0; i < new_len; i += (512 / 8)){
		uint32 state[16] = {0};
		for(unsigned j = 0; j < 16; ++j)
			state[j] = to_uint32(msg + i + j * 4);

		unsigned AA = A, BB = B, CC = C, DD = D, J, f;

		for(unsigned j = 0; j < 64; ++j){
			if(j < 16){
				f = F(BB, CC, DD);
				J = j;
			} else if(j < 32){
				f = G(BB, CC, DD);
				J = (5 * j + 1) % 16;
			} else if(j < 48){
				f = H(BB, CC, DD);
				J = (3 * j + 5) % 16;
			} else{
				f = I(BB, CC, DD);
				J = (7 * j) % 16;
			}
			uint32 tmp = DD;
			DD = CC;
			CC = BB;
			BB += LROTATE(AA + f + t[j] + state[J], s[j]);
			AA = tmp;
		}
		A += AA;
		B += BB;
		C += CC;
		D += DD;
	}
	free(msg);

	to_bytes(hash, A);
	to_bytes(hash + 4, B);
	to_bytes(hash + 8, C);
	to_bytes(hash + 12, D);
}

int main(int argc, char **argv){
	uint8 res[16] = {0};
	md5(argv[1], strlen(argv[1]), res);
	for (int i = 0; i < 16; i++)
        printf("%2.2x", res[i]);
    puts("");
	return 0;
}

运行结果

与在线加密的结果一致

安全性和效率分析

MD5的在测试机上只需要10秒就可以计算完一个500MiB大小的文件的hash值(文件读取不成为瓶颈时)，性能可以接受。

因MD5能够接受的文件大小是$2^{64}$而输出的hash值仅为128位，故必然存在哈希碰撞的问题。现在网上有不少提供反向查询的数据库，通过建立存储有明文-密文对的数据库并查询来得到原象。但是这种攻击的应用场景依然有限，很多时候可以通过加盐来进行保护，故而安全性依旧可以接受在web开发中被广泛使用。

综合实验

需求

Alice想通过公共信道给Bob传输一份机密文件（文件非常大），又知道，很多人和机构想得到这份文件。如果你是Alice，你应该怎样做？

设计

因为要传输的文件非常大，所以选用AES-CBC完成文件传输，平衡安全性和效率。但是如果想做到一次一密这样的理想状态，我们需要建立一个能够用来传送密钥的可信通道。想要建立这样一个可信通道，我选用公钥密码体制来实现，这里用RSA。同时为了防止机构在文件传输中进行篡改，需要对传送的文件的完整性有所保障。这里选用HASH函数配合RSA签名的方案。

详细如下：

  1. Alice 随机生成两个大素数 $p$ 和 $q$ ，计算 $n=p⋅q$ 和 $φ(n)=(p−1)⋅(q−1)$ ，接着计算 $d≡e−1(modφ(n))$ 计算完成后最好立即销毁 $p$,$q$,$φ(n)$，并且确保 $d$ 保密。

  2. Alice 将公钥 $(n,e)$ 发送给 Bob。因为可能存在中间人 Eve ，Bob 需要确定收到的公钥真的是Alice的，这里选择在中立可信的第三方网站上发布自己的公钥，让网站给公钥背书。

  3. Bob随机生成一个长度满足要求的密钥并用Alice的公钥加密发送给Alice。

  4. Alice解密得到这一轮密钥，用AES-CBC对文件进行加密，并把文件的HASH值用自己的私钥签名。加到加密内容的后面发送给Bob。

  5. Bob接收到之后进行解密，用解密得到的明文计算HASH值和签名的HASH值进行比较，如果相等则接受这份文件，否则拒绝并断开连接。

代码实现

密钥生成：

1
2
3
4
5
6
7
8
9
10
def genkey():
    p = getPrime(2048)
    q = getPrime(2048)
    n = p * q
    phi_n = (p - 1) * (q - 1)
    e = 65537

    d = gmpy2.invert(e ,phi_n)
    
    return (n, e, d)

规定p和q的长度为2048bit，应该够用。

AES-CBC所用密钥生成：

1
2
key = os.urandom(16)
iv = os.urandom(16)

从系统的随机数生成器中获取16*8 = 128bit随机值。

接收端做签名验证：

1
2
3
4
5
message = aes.decrypt(cipher)
        hashsum = r.recv(512)
        hashsum = long_to_bytes(encrypt(bytes_to_long(hashsum), e, nn))

        if hashsum == sha1(message):

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
from pwn import *
import hashlib
from Crypto.Cipher import AES
import Crypto.Cipher.AES
import os
from Crypto.Util.number import *
import gmpy2

#context.log_level = 'debug'

def sha1(x):
    m = hashlib.sha1()
    m.update(x)
    return m.digest()

def genkey():
    p = getPrime(2048)
    q = getPrime(2048)
    n = p * q
    phi_n = (p - 1) * (q - 1)
    e = 65537

    d = gmpy2.invert(e ,phi_n)
    
    return (n, e, d)

def encrypt(m, e, n):
    return pow(m, e, n)

def decrypt(c, d, n):
    return pow(c, d, n)

def main():
    ind = raw_input("Am I server / client? [s/c]: ").lower()
    if ind.strip() == 's':
        port = int(raw_input("Port number: "))
        l = listen(port)
        r = l.wait_for_connection()
    else:
        ip = raw_input("Server ip: ").strip()
        port = int(raw_input("Port number: "))
        r = remote(ip, port)

    (n, e, d) = genkey()

    log.success("Generate n: " + str(n))
    log.success("Generate e: " + str(e))
    log.success("Generate d: " + str(d))

    r.send(long_to_bytes(n))

    nn = bytes_to_long(r.recv(512))

    log.success("Get n from another side: " + str(nn))

    ind = raw_input("Send file? [y/n]: ").lower()
    if ind.strip() == 'y':
        key = os.urandom(16)
        iv = os.urandom(16)
        log.success("Generate key: " + str(key))
        log.success("Generate iv: " + str(iv))
        r.send(long_to_bytes(encrypt(bytes_to_long(key), e, nn)))
        r.send(long_to_bytes(encrypt(bytes_to_long(iv), e, nn)))

        aes = AES.new(key, AES.MODE_CBC, iv)

        message = "test"
        length = 16 - (len(message) % 16)
        message += chr(length)*length

        cipher = aes.encrypt(message)
        r.sendline(str(len(cipher)))
        r.send(cipher)
        r.send(long_to_bytes(encrypt(bytes_to_long(sha1(message)), d, n)))
    else:
        key = bytes_to_long(r.recv(512))
        iv = bytes_to_long(r.recv(512))
        key = long_to_bytes(decrypt(key, d, n))
        iv = long_to_bytes(decrypt(iv, d, n))
        log.success("Get key used in this round: " + str(key))
        log.success("Get iv used in this round: " + str(iv))

        aes = AES.new(key, AES.MODE_CBC, iv)
        length = int(r.recvuntil('\n'))
        cipher = r.recv(length)
        message = aes.decrypt(cipher)
        hashsum = r.recv(512)
        hashsum = long_to_bytes(encrypt(bytes_to_long(hashsum), e, nn))

        if hashsum == sha1(message):
            # remove the padding
            message = message[:-ord(message[-1])]
            log.success(message)
        else:
            print("Verify checksum failed, please be careful!")

if __name__ == '__main__':
    main()

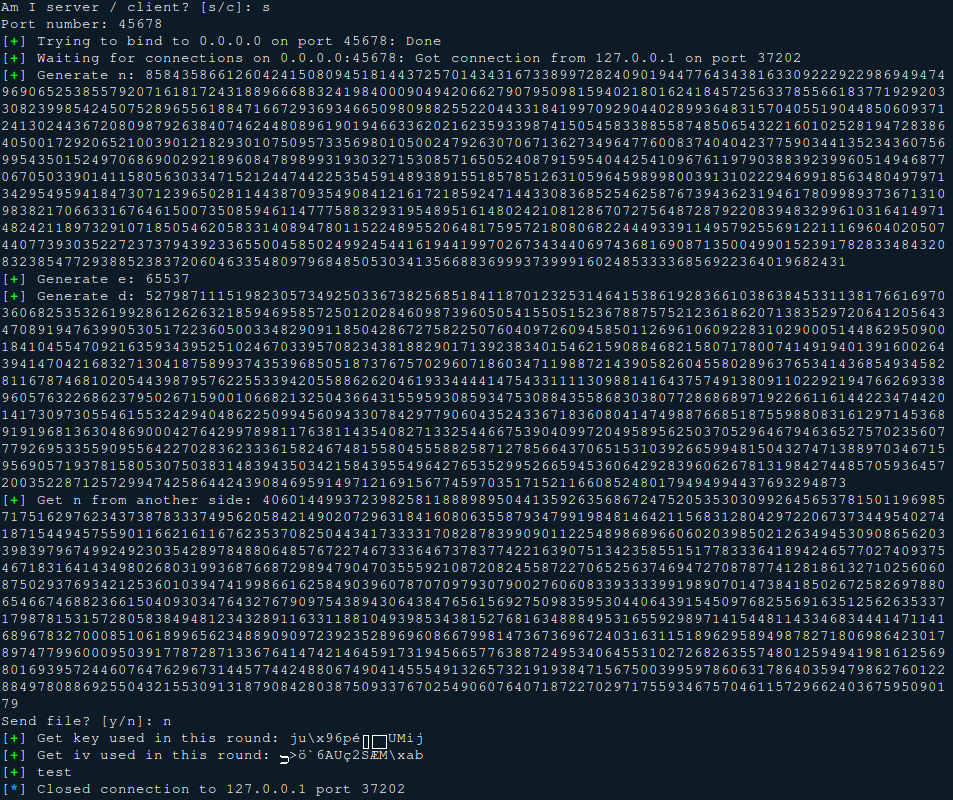
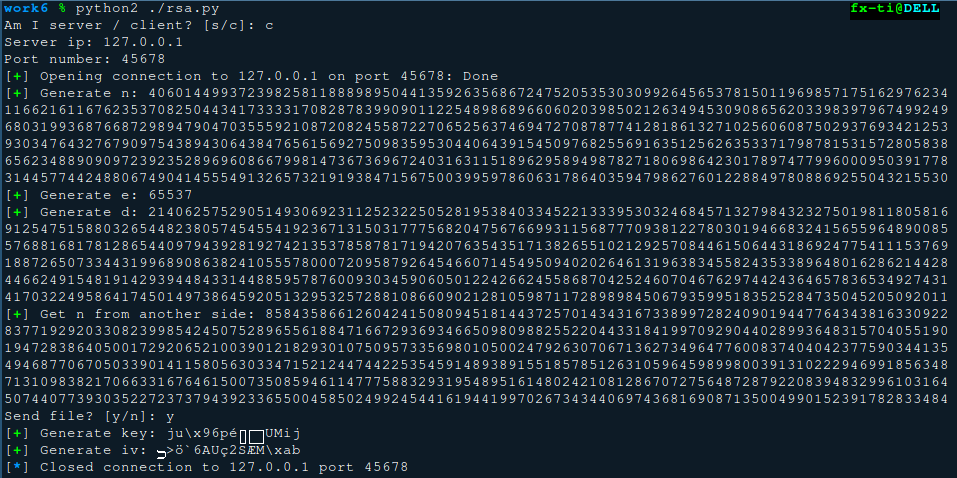
运行截图

服务端：

客户端：